A mecânica utilizada por William Rowan Hamilton foi reformulada seguindo princípios que são fortemente utilizados desde a mecânica clássica, seguindo a origem da mecânica Lagrangeana. Mas, é possível que a mecânica hamiltoniana seja explicada fazendo uso de um estudo de variedades existem que são exclusivas dessa mecânica em questão.
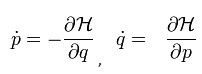
Da mesma forma que a Lagrangeana, a mecânica Hamiltoniana é totalmente capaz de analisar e estudar sistemas mais complexos, (uma capacidade que não existe na mecânica de Newton), mesmo que ela não seja fortemente indicada para alguns casos específicos.
Cálculo Hamiltoniano
As equações que são atualmente utilizadas por Hamilton na intenção de manter um sistema mais conservador, geralmente, para aqueles sistemas que no qual tem algum tipo de alternância periódica, entre energia cinética e a energia potencial, como por exemplo, uma bola batendo em um pêndulo. Porém, ela também é utilizada em um sistema mais complexo, como por exemplo, órbitas planetárias e mecânica quântica.
As duas equações consideradas base da mecânica hamiltoniana são normalmente escritas da seguinte forma como mostra a imagem abaixo:
Nas equações mostradas, = momento linear generalizado em relação ao tempo e = velocidades generalizadas. De modo que:
Repare em uma coisa, observe bem como a função hamiltoniana H, da mesma forma que a função Lagrange, baseada em coordenadas: taxa de variação de um certo momento linear relativo ao tempo, das coordenadas generalizadas em relação ao tempo (velocidades generalizadas) e do tempo, respectivamente.
O sinal negativo que você vai encontrar na segunda equação mostra que a força Newtoniana Variação do momento linear no tempo) se torna igual ao gradiente negativo da energia potencial.
Já a segunda equação, você poderá reparar que a variação das coordenadas no tempo é similar à variação da energia cinética relativa ao seu momento linear.
Função de Hamilton
A função hamiltoniana é dada pela diferença entre a somatória dos produtos no momento considerado linear da partícula e das velocidades gerais:
De acordo com o Lagrangiano dado por esse sistema sendo a diferença entre as energias potencial e cinética da partícula, sempre seguindo os critérios que são recomendados pela mecânica Lagrange.
Sendo mais claro, o Hamiltoniano de um sistema considerado dinâmico é encontrado através da soma T + U, onde T = energia cinética e U = energia potencial. Como vocês já sabem, a energia potencial é dependente da coordenada generalizada, ou posição da partícula sendo mais claro: – U(q) = U(x), a energia cinética pode ser baseada na quantidade de movimentos feitos pela partícula e pela massa que ela representa.
Precisando recorrer a definição da quantidade de movimentos: representada pela relação entre V de uma partícula e sua massa atual M, sendo p = mv. E, sendo energia cinética igual à metade do produto mv², tem-se:
William Rowan Hamilton
Dentre as contribuições para a ciência que foram feitas por esse matemático renomado, nós podemos destacar a teoria dos quaterniões, fundamental nos cálculos de álgebra, e outro é o estudo da refração cônica. Hamilton era um Irlandês, originado de Dublin, nasceu lá em 1805. Ele sempre mostrou ser uma criança prodígio, as 14 anos já dominava os idiomas grego, o latim, o hebraico, o aramaico e o persa.
Ele foi aluno no Trinity College de Dublin, devido ao seu bom histórico escolar e a sua dedicação, futuramente ele veio a se tornar o professor de astrologia no colégio no ano de 1827.
E foi nesse mesmo ano que ele publicou a sua teoria do sistema de raios, onde ele expôs muitas descobertas interessantes sobre óptica, mais especificamente o fenômeno de refração ou absorção parcial da luz pela matéria.
Essa foi a nossa breve explicação sobre a mecânica hamiltoniana e também uma leve descrição sobre a vida de Hamilton, esse matemático Irlandês que fez contribuições incríveis para a ciência.








Comentar