A trigonometria remete aos estudos que iniciaram seu desenvolvimento ainda na Grécia Antiga, a partir dos filósofos matemáticos. Isso não quer dizer, no entanto, que seu conhecimento é ultrapassado – pelo contrário. O uso da trigonometria é utilizado até os dias atuais em uma gama enorme de situações e exigências – desde a construção do dispositivo que você utiliza para ler este artigo agora mesmo, até a construção do local onde você está no momento.
Por isso, entender melhor essa área da matemática é importante não apenas para a aprovação em provas e vestibulares, mas para uma compreensão melhor de todo o mundo ao seu redor. Saiba mais sobre a trigonometria, sua importância e seu significado:
O conceito de trigonometria
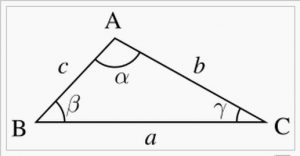
O próprio nome desta área da matemática indica seu significado: e estudo das medidas dos triângulos (trigono + metria). Significa dizer, portanto, que a trigonometria é a área da matemática que dedica-se a estudar as relações e proporções presentes entre lados, ângulos e medidas gerais de um triângulo.
A ideia de conceituação de triângulos em suas diferentes categorias e caraterísticas – como a definição de triângulos retângulos, os ângulos notáveis e o estudo de seno, cosseno e tangente, por exemplo, são resultados do desenvolvimento desta área ao longo da histórias.
Evolução histórica da trigonometria
Há registros históricos de que o estudo de características que hoje são associadas à trigonometria data desde os povos mesopotâmicos e egípcio. Seu desenvolvimento de forma mais consciente e categorizada, no entanto, ganhou força na Índia e na Grécia Antiga.
Na Grécia Antiga, o registro de estudos da trigonometria tem início para medições diversas de distâncias que não poderiam ser feitas na prática. Um dos primeiros nomes associados a estes estudos é o de Hiparco de Niceia, no século II a.C. Hiparco foi um astrônomo e filósofo que começou a pensar na trigonometria como uma ciência propriamente dita, de forma consciente. Nela, dedicava-se a entender as relações constantes nas medidas e elementos de certos tipos de triângulos.
Antes disso, Pitágoras foi um dos grandes nomes relacionados ao desenvolvimento da trigonometria, tendo criado o Teorema de Pitágoras, que dá origem a uma série de estudos e fórmulas adicionais que permitem compreender melhor os triângulos.
Já no século XV, grandes nomes como Isaac Newton dedicaram-se profundamente ao estudo da trigonometria não apenas por si só, mas em suas aplicações práticas – incluindo aspectos muitos mais amplos, como a astronomia.
Foi neste período que a área de estudo consolidou-se dentro da matemática, passando a ser preceito fundamental de diversas ciências exatas. Essa transição permitiu a aplicação em métodos práticos, o que garantiu a evolução de ciências desde a construção civil, até o estudo da astronomia e da cartografia.
Funções trigonométricas
Parte importante da trigonometria é o desenvolvimento de funções trigonométricas. Elas permitem uma compreensão muito mais ampla do mundo e do seu funcionamento, em relação ao aspecto mais técnico.
As funções trigonométricas relacionam-se nos triângulos retângulos – aqueles com um ângulo reto de 90 graus – e nas leis que regem as razões deste triângulo – descobertas pela trigonometria de milênios atrás.
Trata-se do uso dos famosos seno, cosseno e tangente na matemática, nem sempre tão apreciados pelos alunos, mas absolutamente importante para o entendimento do mundo.
Teorema de Pitágoras
Outro tema central dentro da trigonometria é o famoso teorema de Pitágora, criado pelo filósofo grego que batiza teorema ainda cerca de cinco século antes da era comum. Cerca de 2.500 anos atrás, Pitágoras foi capaz de demonstrar que em um triângulo retângulo, a soma dos quadrados do tamanho de seus catetos corresponde exatamente ao quadrado da hipotenusa deste mesmo triângulo.
Essa percepção que parece tão básica é considerada um dos pilares fundamentais da trigonometria e do desenvolvimento do conhecimento matemático como um todo.









Comentar