
Já pensou em desafiar a sua inteligência hoje usando alguns desafios interessantes de matemática? No post de hoje, reunimos para você uma série de joguinhos matemáticos e enigmas lógicos muito loucos que farão você exercitar o seu cérebro ao máximo e colocar o seu QI em prova para solucioná-los e, é claro, se divertir também! Afinal, aprender também é diversão, concorda?
Nos problemas abaixo, será dada a largada para você tentar fazer a mente trabalhar a mil por hora, usando o bom senso, cálculos matemáticos ou macetes inteligentes para encarar os desafios propostos. O mais importante é acertar!
Para testar à quantas anda o seu raciocínio, nós selecionamos os desafios matemáticos e lógicos em três diferentes graus de dificuldade, que podem estar misturados entre fáceis, difíceis e muito difíceis. Está preparado? Vamos começar!
1. Barras de chocolate
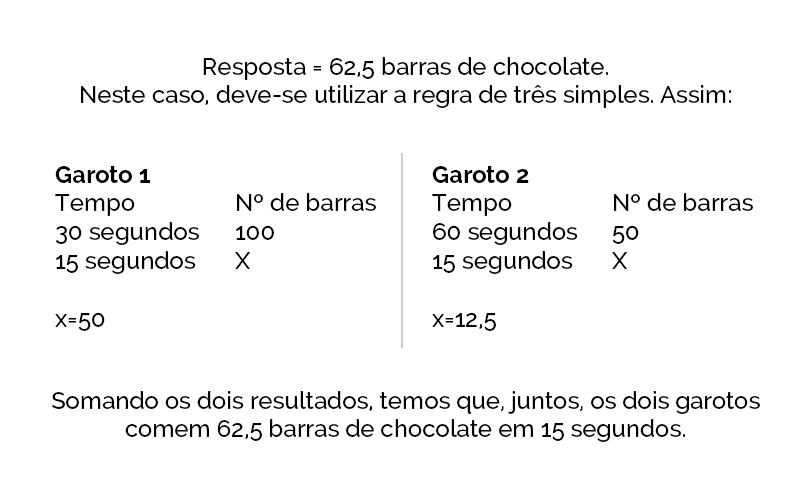
Um garoto consegue comer 100 barras de chocolate em meio minuto. Um outro garoto consegue comer a metade dessa quantidade gastando o dobro desse tempo. Quantas barras de chocolate os dois garotos, juntos, conseguem comer em 15 segundos?
2. Sobe degraus
Uma pessoa se encontra no degrau na metade de uma escada. Sobe 5 degraus, desce 7, volta a subir 4 e depois mais 9 para chegar ao último degrau. Quantos degraus a escada tem?
3. Ida ao museu
Quatro amigos vão ao museu e um deles entra sem pagar. Um fiscal quer saber quem foi o penetra: “Eu não fui”, diz Benjamim. “Foi o Pedro”, diz Carlos. “Foi o Carlos”, diz Mário. “O Mário não tem razão”, diz Pedro. Sabendo que só um deles mentiu, qual deles não pagou a entrada?
4. Número intruso
Observe esses números: 18 – 26 – 35 – 53 – 62 – 71. Qual deles não se relaciona com os demais? Por quê?
5. A travessia
Três homens querem atravessar um rio. O barco que eles possuem suporta, no máximo, 130 quilogramas. Eles “pesam” 60, 65 e 80 quilogramas. Como devem proceder para atravessar o rio, sem afundar o barco?
6. Caracol na parede
Um caracol resolve escalar a parede de um poço de 12 m. A cada dia ele sobe 3 m e, em seguida, escorrega 2 m. Quantos dias ele vai demorar para chegar ao topo do poço?
7. O garrafão de água
Duas pessoas desejam repartir igualmente o conteúdo de um garrafão de 8 litros de água e têm apenas duas garrafas vazias de 5 e 3 litros, além do garrafão. De que maneira eles podem resolver esse problema?
8. A bicharada
Em um sítio existem 21 bichos, entre patos e cachorros. Se, no total, há 54 pés desses bichos, descubra o número de patos e o número de cachorros.
9. Páginas do livro
Se eu leio 5 páginas por dia de um livro, eu termino de ler 16 dias antes do que se eu estivesse lendo 3 páginas por dia. Quantas páginas tem o livro?
10. Cortando a torta
Corte uma torta em 8 pedaços, fazendo apenas 3 movimentos (3 cortes).
11. Palitos de sorvete
Em um certo verão, uma fábrica de sorvetes realizou uma promoção que previa a troca de dez palitos de sorvete por um sorvete de palito. Nessa promoção, um palito de sorvete corresponde a que fração do preço de um sorvete?
12. As lâmpadas
Duas salas estão ligadas entre si por um corredor. Na primeira sala existem três lâmpadas (a, b e c) que estão ligadas a três interruptores (1, 2 e 3) localizados na segunda sala. Como saber que interruptor corresponde a cada lâmpada tendo só uma oportunidade de passar de uma sala para a outra? Considere que não há maneira de espreitar de uma sala para a outra.
13. Os cigarros
Ana Carolina é uma grande fumante, no entanto, decidiu parar de fumar. “Acabarei com os 27 cigarros que sobraram!”, e ainda afirmou: “Jamais voltarei a fumar”. Era costume da Ana Carolina fumar exatamente dois terços de cada cigarro. Não tardou muito em descobrir que com a ajuda de uma fita adesiva poderia juntar três tocos de cigarros e fazer outro cigarro. Com 27 cigarros, quantos ela pode fumar antes de abandonar o fumo para sempre?
14. A pesca
Dois pais e dois filhos foram pescar. Cada um pescou um peixe, sendo que ao todo foram pescados 3 peixes. Como isso é possível?
15. A rolha e a garrafa
Uma garrafa com sua rolha custa R$1,10. Sabendo que a garrafa custa R$1,00 a mais que a rolha, qual é o preço da rolha? E qual é o preço da garrafa?
16. O pássaro e os trens
Dois trens estão no mesmo trilho, indo um em direção ao outro, com uma distância de 100 km entre si. Um dos trens viaja a 40 km/h. O outro viaja a 60 km/h. Um pássaro alça vôo partindo do trem mais veloz, a uma velocidade de 90 km/h. Quando ele alcança o trem mais lento, dá meia volta e voa na outra direção com a mesma velocidade. Quando novamente chega ao trem mais veloz, dá meia volta e torna a voar em direção ao trem mais lento, e assim por diante. Quando os dois trens colidirem, qual será a distância percorrida pelo pássaro?
17. A dízima periódica
Na demonstração matemática a seguir, 10 é igual a 9,99999…. O que há de errado com ela?
a = 9.999999…
10a = 99.999999…
10a – a = 90
9a = 90
a = 10
18. 2 igual a 1
Na demonstração matemática a seguir, 2 é igual a 1! O que há de errado com ela?
a = b
aa = ab
aa – bb = ab – BB
(a + b)(a – b) = b(a – b)
a + b = b
a + a = a
2a = a
2 = 1
19. Fatorial de 50
Explique, sem realizar efetivamente o cálculo, porque 30414093201713378043612608166064768844377641568960512078291027000 não pode ser o valor de 50! (50 fatorial).
20. Números ocultos
Quais são os 2 números cujo produto é 48 e, quando o número maior é dividido pelo menor, obtém-se quociente 3?
21. Soma no jogo da velha
Organize os números de 1 a 9 em um tabuleiro de jogo da velha (como o da figura abaixo), de tal forma que a soma dos 3 números de cada coluna, de cada linha e de cada diagonal seja sempre 15.
Dica: Coloque o número 5 no meio do tabuleiro.
__|__|__
__|__|__
| |
22. Galinhas e coelhos
Há algumas galinhas e alguns coelhos numa gaiola (não há aí nenhum outro tipo de animal). Há 72 cabeças e 200 pés dentro da gaiola. Quantas galinhas e quantos coelhos existem lá?
23. A baleia
Uma baleia tem 15 metros de comprimento. Sua cabeça é tão grande quanto sua cauda. Se a cabeça fosse duas vezes mais comprida do que realmente é, a cauda e a cabeça, juntas, seriam tão compridas quanto o resto do corpo da baleia (ou seja, a parte que está entre a cauda e a cabeça). Qual é o comprimento de cada parte do corpo da baleia?
24. Peso das batatas
As batatas possuem, em sua constituição, 99% de água e apenas 1% de “material de batata”, propriamente dito. João comprou 100 kg de batatas e as deixou no quintal, tomando um “banho de sol”. Quando ele voltou, viu que as batatas haviam desidratado e possuíam, agora, apenas 98 % de água em sua composição. Naquele momento, qual era o novo peso das batatas?
25. Amarrando o mundo
Um indivíduo excêntrico fez do seu objetivo de vida amarrar uma corda em torno da linha do equador. Ele comprou uma grande porção de corda e fez uma tentativa. Um rival seu, para não ficar para trás, decidiu amarrar uma corda ao longo do equador terrestre, só que 1 metro acima (em altura) da linha do equador, ou seja, a corda será passada a um metro de altura do chão. De quantos metros de corda a mais ele irá precisar? Considere a Terra como sendo uma esfera perfeita.

































Comentar