Poliedros são formas tridimensionais da geometria especial. Isso significa que são sólidos com comprimento, largura e altura, que formam vértices, arestas e faces. Embora possam ser uma das partes mais interessantes da matemática, poliedros podem ser o pesadelo de alguns estudantes.
Não há, no entanto, motivo para isso: aprendizado e simples e exige apenas uma pouco de percepção e conhecimento básico das fórmulas de geometria. Por isso, separamos um guia básico sobre poliedros, a Relação de Euler, as diferenças entre pirâmides regulares e irregulares e suas curiosidades.
Saiba mais sobre o assunto e suas principais características:
Definição de poliedros
Um poliedro é definido, sobretudo, pela formação de polígonos unidos, sendo o polígono formado por n lados, sendo que seus lados formam vértices e arestas. Esta é, em resumo, a definição mais básica de um poliedro: uma forma tridimensional composta por polígonos.
Poliedros regulares e irregulares
Os poliedros podem ser divididos em duas classes: regulares ou não regulares. Em resumo, pode-se considerar os regulares como aqueles cujas faces é são formadas por polígonos regulares e necessariamente congruentes. Os não regulares também são formados por polígonos regulares, mas incluem polígonos irregulares em sua composição.
Poliedros regulares
Os poliedros regulares são aqueles chamados de sólidos platônicos, com faces formadas por polígonos regulares. São considerados cinco poliedros de Platão:
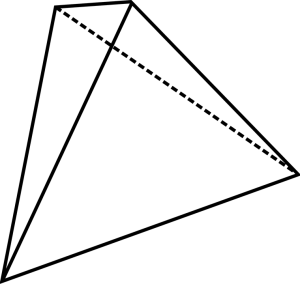
O tetraedro é um sólido formado por quatro faces triangulares, que geram quatros vértices e seis arestas. O hexaedro, também chamado de cubo, conta com seis faces quadrangulares, oito vértices e doze arestas.
O octaedro é formado por oito faces triangulares, seis vértices e doze arestas. O dodecaedro é formado por doze faces pentagonais, 20 vértices e 30 arestas. O icosaedro, por sua vez, é o sólido formado por vinte faces triangulares, gerando doze vértices e trinta arestas.
Poliedros não regulares
Diferentemente dos poliedros regulares, os não regulares combinam, em suas faces, polígonos regulares e irregulares. Isso forma dois exemplos mais comuns, geralmente utilizados em exercícios: o prisma e a pirâmide.
Tratam-se, de maneira simplificada, de sólidos que mesclam diferentes polígonos. No caso do prisma, há laterais quadriláteras, inferior plano e congruente e duas faces triangulares. Já as pirâmides conta com um polígono de n lados em sua base, e triângulos que partem da aresta de cada um destas lados. A definição de uma pirâmide exige, ainda, que estes triângulos encontrem-se em um único vértice no lado oposto ao polígono de base.
Teorema de Euler
O Teorema de Euler, também chamado de Relação de Euler, é válido para a definição matemática de todos os poliedros regulares. Ele não é, no entanto, aplicável naqueles que não são regulares, por a relação perde sua natureza proporcional. Isso porque, nos sólidos regulares, há a mesma quantidade de arestas para cada vértice formado.
Desta forma, é possível definir que, considerando-se que F define o número de faces, V define o número de vértices e A define o número de arestas:
F + V = 2 + A
Ou, então:
V – A + F = 2








Comentar