O nome progressão aritmética pode parecer complicado o suficiente para assustar aqueles menos próximos à matemática. Na prática, no entanto, a resolução de exercícios de progressão aritmética é bastante simples, e é comum que utilizemos este tipo de conhecimento em nosso dia a dia, sem nem mesmo percebermos que trata-se de um exercício do tipo.
Uma progressão aritmética nada mais é do que uma sequência de números estabelecida a partir de uma lógica que repete-se entre todos os termos. O fato de ser constante é o que torna tal progressão aritmética.
Saiba mais sobre o assunto, e entenda como o conteúdo de progressão aritmética pode ser simples:
O que é uma progressão aritmética?
Uma progressão aritmética é uma sequência numérica regida por uma lógica constante de progressão. A esta lógica é dado o nome de razão. A razão é a constante definidora de qual valor será acrescido em relação a todo termo prévio de uma sequência para que ela progrida.
Para exemplificar uma progressão aritmética, pode-se pensar em uma sequência iniciada pelo número 1 com razão de 3. Neste caso, pode-se entender que a progressão em questão é formada pela sequência:
(1, 4, 7, 10, 13, 16, 19, 21, 24…)
Tipos de progressão aritmética
Existem diferentes tipos de progressões aritméticas, que são definidas pela natureza de sua razão. Elas são classificadas em três formas distintas:
Progressão crescente
Uma progressão aritmética crescente é aquela que possui uma razão positiva. A razão, portanto, sempre será superio a zero, fazendo com que a sequência torne-se cada vez maior, a depender do valor definido.
Progressão decrescente
Uma progressão decrescente é aquela na qual, ao contrário do exemplo anterior, a razão é negativa, definida como r < 0. Isso significa que cada novo termo da sequência será menor que o termo anterior. Nos casos em que a sequência é infinita, essa progressão seguirá em números negativos de valor cada vez mais significativos.
Progressão constante
Uma progressão constante é aquela em que todos os termos são iguais. Trata-se, portanto, de uma não progressão, a depender da definição. Ela só existe a partir de uma condição: sua razão ser nula, ou seja, r = 0.
Definições de uma progressão aritmética
Uma progressão aritmética pode ser formulada a partir de um termo geral, no qual a representa os termos da sequência, n representa o número do termo em relação à sequência, e r, por óbvio, representa a razão. Neste caso, a fórmula geral é definida por:
PA = (a1, a2, a3, a4, a5…) onde a2 = a1 + r
Além disso, é possível definir qualquer termo de uma progressão aritmética pela fórmula:
an = a1 + (n – 1)*r
Propriedades de uma progressão aritmética
Existem algumas propriedades constantes que podem ser observadas em relação a qualquer progressão aritmética definida a partir dos termos anteriores, que facilitam sua compreensão em circunstâncias variadas.
Em primeiro lugar, pode-se definir que exceto o primeiro termo de uma PA, qualquer um de seus termos é a média entre o termo anterior e o termo posterior a ele próprio. Isso se dá em função da natureza constante da racionalidade envolvida na sequência, onde a variação dos termos representa exatamente a variação de razão.
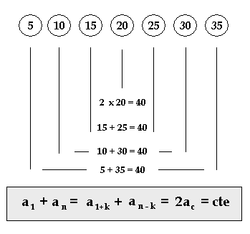
Outra propriedade interessante é o fato de que a soma de quaisquer dois elementos equidistantes em relação aos extremos da sequência (desde que finita) dará sempre um mesmo resultado.
Significa dizer que a soma entre o primeiro e o último número de uma sequência possui o mesmo resultado que a soma entre o segundo e o penúltimo, que dará o mesmo resultado que a soma entre o terceiro e o antepenúltimo.
Por último, pode-se considerar que em uma progressão aritmética com quantidade ímpar de termos, o elemento central sempre representará a média aritmética dos extremos desta sequência.









Comentar