O conteúdo de matrizes assombra muitos alunos no ensino médio, e tantos outros estudantes para concurso e, até mesmo, na faculdade. A verdade é que o conteúdo não é tão rapidamente compreensível quanto os aprendidos até então, pois trata de uma espécie de nova dimensão matemática.
Com um pouco de prática e familiaridade, no entanto, tudo torna-se mais fácil. Entender matrizes não é tão complicado, e basta entender alguns tipos e regras básicas para que se possa utilizar elas de maneira eficiente.
Entenda mais sobre o conteúdo de matrizes, seus tipos e as operações que podem ser realizadas com elas:
O que é uma matriz?
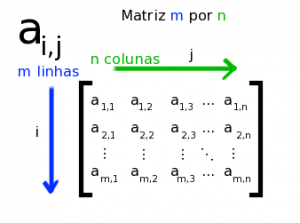
De forma extremamente simplificada, pode-se dizer que uma matriz é nada mais do que uma tabela. Quando representada por uma matriz de m x n indica que ela terá m linhas por n colunas. Tratando-se de uma matriz X de 1 x 2, onde suas colunas são (5) e (10), o resultado é a extremamente pequena:
X = [5 10]
Fosse uma matriz X de 2 x2 e as colunas fossem (5, 50) e (10, 100):
X = [ 5 10] [50 100]
Dentro de uma matriz, é possível indicar a localização de seus elementos. No caso de X, pode indicar que 10 encontra-se no elemento x1×2, dada sua notação onde Xmxn indicam linhas e colunas respectivamente.
Tipos de matrizes
É importante compreender que existem diferentes tipos de matrizes. Entre eles, destacam-se:
Matriz transposta
É aquela em que os vetores de colunas convertem-se em linhas. Uma matriz transposta só existe considerando-se a existência de outra matriz original. Utilizando nosso exemplo da matriz X, teríamos que X transposta é:
Xt = [ 5 50] [10 100]
Matriz nula
Uma matriz nula é aquela em que todos os seus vetores, independentemente da quantidade de linhas e colunas, são nulos. Isso significa que ela é completamente formada por zeros.
Matriz quadrada
Uma matriz quadrada é aquela que possui a mesma quantidade de linhas e colunas. Ela é, nestes casos, uma matriz quadrada de ordem n, onde n equivale à quantidade de colunas e linhas. Nosso exemplo de matriz X, de 2×2 é uma típica matriz quadrada de ordem 2.
Operações entre matrizes
As operações entre matrizes são muito semelhantes àquelas entre vetores. É necessário, para isso, considerar cada elemento da matriz para realizar a operação.
Por isso, no caso de uma soma entre matrizes, soma-se cada um dos elementos equivalentes:
[ 5 10] [ 5 10] [10 20] [50 100] + [50 100] = [100 200]Na multiplicação, utiliza-se a mesma lógica do caso anterior. Exemplificando-se com as mesmas duas matrizes sendo multiplicadas em vem de somadas, o resultado seria:
[ 25 100 ] [2.500 10.000]O produto de uma multiplicação entre duas matrizes, no entanto, é um conteúdo que precisa ser compreendido à parte, pois torna-se um pouco mais complexo e exige atenção exclusiva.
As outras operações, é claro, seguem a mesma lógica de utilização, e geralmente são expressas através de frações ou números negativos dentro de uma mesma matriz.








Comentar