No que tange os conjuntos numéricos, os números irracionais provavelmente representam os mais confusos para os estudantes mais jovens. Trata-se de um conjunto entendido dentro dos Reais, mas que não são obtidos através da divisão de Números Inteiros.
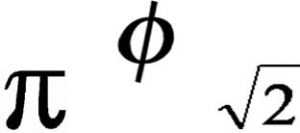
Entenda como são definidos os Números Irracionais, sua obtenção e classificação prática:
O que são os Números Irracionais?
A expressão números irracionais é dada ao conjunto numérico representado pela letra I. Os números irracionais são parte do conjunto dos Números Reais, em um conjunto distinto, por óbvio, dos grupos irracionais.
Significa dizer, portanto, que os Números Reais são compostos por dois Conjuntos e suas subdivisões: os Números Irracionais e os Números Racionais (Q).
Os Irracionais não pode ser representados por frações comuns, uma vez que é impossível que resultem de uma divisão entre dois Números Inteiros. São sempre representados, portanto, como números que utilizam-se de casas decimais de forma infinita e não periódica.
É o caso de Pi, por exemplo, assim como todas as outras dízimas não-periódicas.
Quem conceituou os Números Irracionais?
O surgimento dos Irracionais para a matemática remonta a filosofia grega. Mais especificamente, os tempos de estudo da Geometria. A primeira vez que foram demonstrados, na verdade, foi a partir da utilização de cálculos geométricos. Fala-se que foi necessário que um dos seguidores de Pitágoras demonstrasse sua existência.
O Teorema de Pitágoras apresenta uma máxima muito conhecida: em um triângulo reto, a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa. Em um exemplo clássico, entende-se que um triângulo de lados 3 e 4 terá uma hipotenusa de 5, considerando a regra geral.
Há, no entanto, a possibilidade de um triângulo de lados 1 e 1. Neste caso, a soma do quadrado dos catetos é 1 + 1. Obriga-se, portanto, que o quadrado da hipotenusa seja dois. A diagonal do triângulo corresponderá, desta forma, à raíz quadrada de 2.
Não há um número racional que represente a raiz quadrada de dois, pois trata-se de um número infinito e inconstante. Trata-se do número 1,414213562373…, com prosseguimento infinito e não padronizado.
Trata-se de uma situação muito menos compreensível do que a divisão de 10 por 3, que resulta em um número infinito, porém constante (uma dízima periódica, compreendida como Racional). Assim foi definida a existências dos Número Irracionais, que são parte dos Reais, mas diferentes dos Racionais.
A constante de Arquimedes
Outro fator importante para a compreensão plena dos Números Irracionais foi feita em relação à circunferência de uma forma redonda. Deste cálculo, foi definido o mais famoso dos número irracional: o Pi.
O número Pi corresponde sempre a um número irracional (portanto, infinito e inconstante), de valor 3,141592…
Isso ajuda a exemplificar que os Irracionais são parte do conjunto dos Reais, pois são encontráveis de maneira prática na matemática e na natureza. O mesmo pode ser dito a respeito do “número de ouro”, que determina a razão sequencial de Fibonnacci, e é replicada em diversos exemplos da natureza.









Comentar