Relações e funções: o que são?

Relações e funções são temas importantes da matemática, e fazem parte de assuntos que permitem uma compreensão mais ampla do tema e de seus aprendizados. Aprender sobre o tema é bastante simples, uma vez que relações e funções não necessariamente exigem a realização de cálculos complexos.

A própria utilização da nomenclatura relações e funções demonstra que estes conteúdos são bastante relacionados à compreensão da natureza de fatores matemáticos, e não ao seu cálculo como a finalidade plena.

Basta entender sua lógica de funcionamento para uma correta configuração de análise de relações e funções. Confira:

O que é uma função?

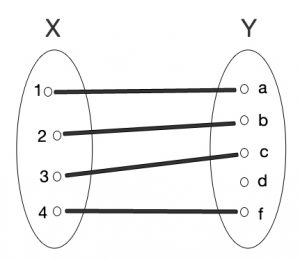
Um função é uma definição matemática na qual correlacionam-se dois domínios. O primeiro é chamado de domínio, e o segundo é chamado de contradomínio, correspondendo a valores de saída que existem em função dos valores de entrada do primeiro domínio.

Cada elemento do domínio está diretamente relacionado a um elemento do contradomínio, sendo que o conjunto de elemento que correspondem a uma relação dentro deste contradomínio é chamado de imagem.

Desta forma, torna-se correto dizer que um elemento da imagem é relacionado em função do elemento x do domínio. É exatamente neste contexto que surge a forma de representação gráfica entre domínios, na qual se estabelece que uma função pode ser definida como f(x), pois todo resultado da imagem é obtido em uma função de x, sendo x um elemento do domínio.

O que é uma relação?

Uma relação é uma correspondência, um vínculo existente entre dois referenciais. No caso da matemática, uma relação é uma correspondência que pode existir entre dois conjuntos determinados. Tratando-se de uma função, especificamente, pode-se dizer que há relação entre imagem e domínio, mas não necessariamente existe relação entre contradomínio e domínio, uma vez que não é obrigatório que todos os elementos deste contradomínio sejam relacionados ao domínio.

Tratando-se de relações e funções, no entanto, vale deixar claro que um elemento de conjunto deve corresponder a apenas um outro. Não é possível que um elemento do domínio tenha relação com mais de um elemento da imagem, por exemplo. É possível, por outro lado, que um elemento da imagem seja a correspondência de dois elementos diferentes do domínio.

Toda essa linguagem complexa usada para definir uma relação e suas regras remetem a uma única característica final: uma relação matemática é precisamente a mesma coisa que uma função matemática!

Então porque existem dois nomes

Fora a obviedade de que simplesmente pudessem existir duas nomenclaturas distintas para uma mesma coisa, há outras explicações que podem facilitar a compreensão do uso de relações e funções na linguagem matemática.

Quase sempre que falamos em relações, provavelmente estaremos tratando diretamente das relação e conjuntos, graficamente representados em domínio, contradomínio e imagem, da forma como aprendemos na escola. Quando fala-se apenas em funções, é muito comum que já estejamos pensando em uma aplicação mais algébrica deste conteúdo.

Deve-se deixar bem claro que essa não é uma definição oficial, mas um consenso utilizado no dia a dia para definir uma área do conhecimento que pode ser aplicada de diferentes maneiras.