Os tipos de funções podem ser uma memória bastante desagradável para muitos alunos que não são tão fãs da matemática. A verdade, no entanto, e que o conteúdo não é muito difícil, Na prática, entender os tipos de funções exige percepção e atenção, sem a necessidade de cálculos complexos ou níveis avançados de matemática propriamente dita.
Para compreender os tipos de funções existentes, é necessário saber as características de cada uma, e o que as define. Confira o guia rápido dos diferentes tipos de funções, e quando identificar cada um deles:
Classificações quanto ao tipo
As classificações quanto ao tipo determinam a forma como um variável que existe em função de outra comporta-se em relação a ela. Os três tipos considerados de funções são:
Funções injetoras
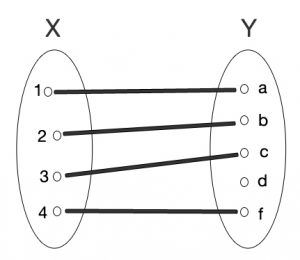
A função injetora é aquela em que um elemento do domínio analisado pode ser associado a apenas um elemento no domínio imagem, como define a regra geral do assunto. Nas funções injetoras, no entanto, é possível que – a despeito da correlação entre elementos – o contradomínio contenha elementos que não digam respeito ao elementos da função.
Isso quer dizer que é um conjunto pode ter três elementos, enquanto o contradomínio pode apresentar cinco, sendo que dois deles não fazem parte da imagem da função do conjunto original.
Funções sobrejetoras
Uma função sobrejetora é aquela na qual todos os elementos do contradomínio e da imagem correspondem entre si – o que quer dizer que todos estes elementos dizem respeito a um elemento do domínio da função.
Pode-se dizer que não “sobra” nenhum elemento do contradomínio, diferentemente das funções injetoras. O que caracteriza as sobrejetoras, neste caso, é o fato de que um elemento da imagem pode corresponder a mais de uma elemento do domínio da função. Pode haver, portanto, cinco elementos no domínio da função e apenas quatro elementos no imagem, correspondendo a todos eles.
Funções bijetoras
As funções bijetoras são aquelas que reúnem característica injetoras e sobrejetoras. São injetoras na medida em que todos os elementos da função possuem relação com um único elemento na imagem, sem que um elemento do contradomínio seja relacionado a dois elementos da função.
Possui características sobrejetoras, no entanto, no que diz respeito ao fato de que o contradomínio e a imagem são idênticos. Isso significa que não “sobra” nenhum elemento do contradomínio em relação à imagem. A soma destas características em uma função, faz dela uma bijetora.
Tipos de funções quanto ao grau
Outra forma de se definir os tipos de funções é a identificação dos graus aos quais elas correspondem. O grau de uma função é determinado pelo grau da potência aos quais os elementos são elevados. Isso porque os elementos com potências diferentes não podem ser diretamente calculados entre si, adicionando uma camada de complexidade em sua resolução.
No caso de uma função de primeiro grau, sabemos existir um incógnita em primeiro grau. No caso de uma função de segundo grau, portanto, entende-se que a incógnita é elevada à segunda potência – ou ao seu quadrado – e esta lógica de classificação segue em diante.









Comentar