Para muitas pessoas, pensar em fatoração em uma prova é um processo complexo e assustador. Não é sem motivos: muitas vezes, o processo de ensino da fatoração torna tudo muito mais complicado.
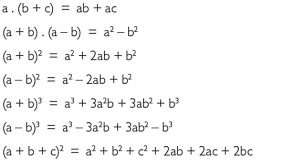
Na prática, no entanto, o tema pode ser muito mais simples do que parece. Na verdade, a fatoração foi criada exatamente com a intenção contrário: ser uma simplificação de sentenças matemáticas. Em outras palavras, transformar soma e subtração de uma equação em um produto com fatores.
Na matemática, considera-se sete casos diferentes de fatoração. Entender cada um deles facilita significativamente o domínio do conceito, permitindo que a fatoração nunca mais assuste você. Confira:
Fator comum
O fator comum é o primeiro caso, onde um dos termos repete-se nos monômios contidos na expressão. É o caso do exemplo:
ax+bx = x⋅(a+b)
Neste caso, o termo “x” deve ser colocado em evidência, como feito após o sinal de =, pois repete-se em ax e bx. É importante compreender que o fator comum a ser colocado em evidência pode ser qualquer tipo, não sendo necessário que tenha o caráter de incógnita.
Em uma expressão 2x + 2y, por exemplo, a forma de fatoração seria 2(x + y).
Agrupamento
Este é o segundo caso de fatoração. Sua intenção é reunir os termos comuns em partes da expressão. Trata-se de um procedimento semelhante ao primeiro caso, mas que é utilizado em equações onde um termo não está presente em todos os monômios. É o caso típico da equação:
ax+bx+ay+by
Neste caso, a fatoração por agrupamento leva ao resultado:
(x+y)⋅(a+b)
O importante, neste caso, é observar a reunião dos termos comuns entre si, a despeito de sua não repetição em toda a expressão algébrica.
Trinômio do quadrado perfeito
O trinômio quadrado perfeito é a terceira regra de fatoração. Ele é o inverso do processo de produtos notáveis. Ela só pode ocorrer com trinômios que sejam quadrados perfeitos. Neste caso, fatora-se os termos de forma bastante fácil.
É o caso do trinômio quadrado perfeito x2 +2xy + y2 que, fatorado, toma a forma (x + y)2.
Diferença de dois quadrados
Em expressões que contem com dois monômios elevados ao quadrado que estiverem em operação de subtração, é possível realizar a fatoração de diferença de dois quadrados. Um de seus exemplos mais clássicos é a expressão:
x2 – 4
Neste caso, a raiz quadrada dos dois termos são, respectivamente, x e 2. Por isso, realiza-se sua fatoração através da operação de diferença dos quadrados. Sua forma fatorada é:
(x – 2) (x + 2)
Demais regras de fatoração
Há, ainda, outras três regras distintas de fatoração previstas na matemática. Diferentemente destes casos, elas são menos comum e exigem um espaço próprio para explicação, não sendo possível repassar seu conteúdo em tópicos rápidos e resumidos.
São estas três a regras as fatorações de trinômico do tipo x² + Sx + P, da soma de dois cubos e da diferença de dois cubos. É necessário levar em consideração que as três regras são significativamente importantes, e não devem ser ignoradas. O único motivo pelo qual não são explicadas aqui é sua maior demanda por um espaço próprio.









Comentar