No mundo da física teórica, a terceira lei de Kepler é mais conhecida como a lei dos períodos ,e foi desenvolvida cerca de dez anos após a lei das áreas (segunda lei de Kepler). Essa lei demonstra a relação diretamente proporcional entre o período de revolução de um planeta em torno do sol e o raio médio da orbita do planeta. Por isso, é considerada relevante no entendimento do comportamento de nosso próprio planeta. Ela pode ser descrita da seguinte maneira:
“Os quadrados dos períodos de revolução dos planetas em torno do sol são diretamente proporcionais aos cubos dos raios médios de suas orbitas.” Assim, sendo T o período de revolução e de R o raio médio da orbita, temos:
T2 = Constante
R3
Entenda melhor o significado dessa importante fórmula, e como ela auxiliou a explicar a movimentação dos planetas em nosso sistema solar:
O que a terceira lei de Kepler determina?
Essa conexão demonstra que, quanto mais longe um planeta estiver do sol, maior haverá um tempo de revolução ao redor da estrela. Sendo assim também para todos os nossos planetas do sistema solar, a relação acima contem praticamente o mesmo valor.
Foi possível postular um único princípio com a Teoria da Gravitação Universal de Isaac Newton que, aliado às Três Leis de Newton, foi capaz de explicar totalmente as analises astronômicas conhecidas até a época e ainda depois, até a descoberta de que a velocidade da luz no vácuo é constante para todos os tipos de referenciais.
Essa descoberta caminhou à criação da teoria da relatividade restrita e, consequentemente, da teoria da relatividade geral, que, para alguns fenômenos que até então não tinham sido observados, invalida a teoria de Newton da gravitação.
No entanto, as leis de Newton e a sua teoria da gravidade são mais do que suficientes para desmembrar as leis de Kepler. As três leis são deriváveis da simples equação postulada acima de fato, e de modo que ainda aparecem mais completas do que da forma descrita por Kepler.
Kepler e as órbitas solares
Sabe-se que as órbitas dos planetas são elípticas, entretanto, para a dedução da Terceira Lei de Kepler, iremos levar em consideração uma órbita circular. Os resultados também valem para órbitas elípticas, apesar da demonstração a seguir ser feita tomando como base órbitas circulares.
Na figura abaixo nós temos um planeta girando ao redor do Sol. Essa força centrípeta (Fc) é uma força de origem gravitacional de atração realizada pelo Sol. As forças de atração realizadas sobre planetas e satélites são desprezíveis, isso por conta do fato de suas massas serem muito inferiores à massa do Sol.
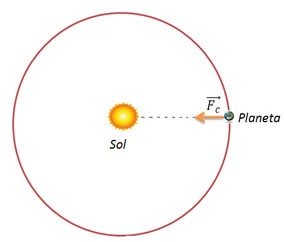
Como o planeta de massa (m) orbita ao redor do Sol, em um movimento circular e com velocidade angular, a força resultante sobre o planeta, chamada força centrípeta (Fc), é dada por:
Fc=mω2 r
Em que:
Fc: força centrípeta;
m: massa do planeta;
ω: velocidade angular do planeta;
r: raio da órbita do planeta.
T: tempo decorrido
A velocidade do ângulo, para fins de cálculo, é dada por duas vezes o pi sobre o tempo decorrido durante o trajeto calculado, obedecendo a noção de força centrípeta anterior.









Comentar