A geometria analítica é a área da matemática dedicada ao estudo de geometria através da álgebra. Para muitas pessoas, trata-se do conteúdo de colégio associado a coordenadas geométricas em um plano visual.
Os primeiros estudos matemáticos sobre a geometria analítica foram desenvolvidos pelo matemático e filósofo René Descartes, no século XVII. Foi ele o responsável pelo sistema gráfico de coordenadas cartesianas, utilizadas até hoje pela geometria analítica.
Saiba mais sobre esta área do conhecimento, como ela foi criada e seus principais conceitos:
O que estuda a geometria analítica?
A geometria analítica dedica-se ao estudo de conexões ente álgebra e geometria. Em outras palavras, trata-se do potencial de análise dos temas e formas da geometria através de um processo algébrico propriamente dito. A forma de associação mais comum desta área do conhecimento é a geometria cartesiana.
Isso significa que as figuras clássicas da geometria plana – e até mesmo espacial – podem ser convertidos sob um prisma algébrico para o que se chama “processo analítico”, que permite uma compreensão muito mais da própria geometria.
História da Geometria Analítica
O início da Geometria Analítica por si só data do século XVII, período em que houve um nova onda de dedicação matemática de alta intensidade. O principal responsável por ela foi o matemático Descartes, que reuniu conceitos da Álgebra e da Geometria para analisar propriedades de pontos e coordenadas, graficamente distribuído em um plano visual com localização e características geométricas.
Outros pensadores profundamente envolvidos com a geometria analítica foram Issac Newton e Wilhelm Leibniz, cujas obras possuem enorme extensão no uso cotidiano da matemática. Leibniz, por exemplo, utilizou o conteúdo como base para o desenvolvimento do cálculo diferencial e integral, conteúdo não aprendido no Ensino Médio atual, mas companheiro dos primeiros semestres de todos os cursos de engenharia.
Principais características da geometria analítica
Desde sua criação, este conteúdo trata basicamente de uma definição numéria das formas geométricas, representando-as das duas formas como sinônimos. É justamente a partir dessas possibilidades que o pensamento sobre conceitos como vetores surgem, dando espaço a estudos espaciais, no sentido de considerar tamanho, direção e sentido na matemática – o que, por óbvio, é absolutamente importante na física e na engenharia.
Essas possibilidades permitem dizer que a geometria analítica, em grande medida, deu início à matemática que pode ser considerada como moderna. Trata-se da matemática de matriz iluminista, rompendo-se da tradição essencialmente grega consolidada até então.
Conceitos básicos da geometria analítica
Sob o ponto de vista mais básico possível, pode-se definir o processo de análise algébrica da geometria como a representação dos pontos de uma reta ou forma através de uma viés matemático. Significa atribuir números reais à existência de um ponto de uma reta, por exemplo. Cada ponto desta reta corresponde a um número relacionado aos pontos anteriores. Isso significa que pode-se converter uma distância em uma equação, ou o processo inverso, pois existem representações gráficas ou algébricas destas formas.
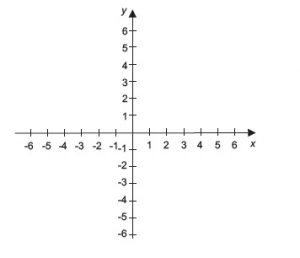
Por isso, é necessário estabelecer o “cenário” onde a geometria analítica ocorre. Trata-se do plano cartesiano, composto por dois eixos. Estes eixos podem ser considerados como vertical e horizontal, graficamente representados como tal. Pode-se estabelecer quatro quadrantes a partir destas retas, sendo que cada um deles representa aspectos de característica negativa ou positiva em relação a estes eixos, uma vez que o ponto central de intersecção entre eles é considerado o valor 0, tanto horizontalmente quanto verticalmente.
Desta forma, cada ponto traçado neste plano cartesiano possui duas informações de coordenadas – uma sobre sua posição horizontal, e outra sobre sua posição vertical. Assim, todo ponto pertencente ao plano em questão possui um valor em coordenadas, recebendo duas dimensões que podem ser fisicamente compreendidas, mas que são numericamente estabelecidas. É dessa forma que se pode converter questões geométricas e algébricas em um mesmo assunto.








Comentar