Os números racionais eram, até determinado ponto da história grega, considerados todos os tipos de números existentes. Com o passar do tempo e a evolução da filosofia, no entanto, foi possível perceber uma distinção entre os racionais e os irracionais, de forma que a matemática pudesse evoluir significativamente.
Hoje, o conjunto de números racionais é compreendido como a “metade mais cotidiana” do conjunto de números reais, ao qual pertence. Além dos números fracionários, os racionais compreendem números inteiros – positivos ou negativos – que possam ser definidos através de frações matemáticas.
Entenda melhor a definição, a classificação e algumas informações sobre os números racionais:
Definição de números racionais
Os números racionais podem ser expressos como o quociente de dois inteiros (em outras palavras, uma fração), desde que o denominador da operação não seja zero.
Isso significa que todos os números frutos de divisões não denominadas por zero que resultem em algo diferente de uma dízima não periódica pode ser considerado, grosso modo, racional. Quando fala-se em números resultantes de frações, isso não significa que o número precise apresentar casas decimas que não sejam zero para ser considerado racional. Números inteiros também fazem parte deste conjunto.
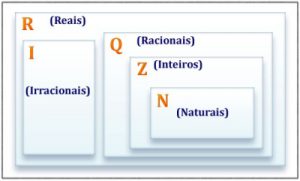
Quais conjuntos numéricos fazem parte dos números racionais?
Segundo as definições de conjuntos, na matemática, define-se que o números racionais compreendem, ainda, os números naturais e os números inteiros, além – é claro – dos puramente racionais. Além disso, todo número racional é considerado parte de um conjunto maior, dos números reais.
Isso significa que um número natural é, consequentemente, inteiro, racional e real. Um número inteiro é sempre racional e real, e um número racional é, necessariamente real.
O que são os números irracionais?
Os número irracionais são aqueles compreendidos como números reais, mas que não fazem parte dos racionais. Exemplos famosos de números irracionais são a raiz quadrada de dois e o número Pi – assim como todas as outras dízimas não-periódicas.
Se os números racionais são aqueles que podem ser definidos através de uma fração simples (como 1/3, 4/4 ou até mesmo 1,5/4,72), os irracionais são aqueles que não podem ser matematicamente expressos dessa forma. Não há forma de definir a raiz quadrada de dois através da divisão de dois números, por exemplo, o que o torna, por definição, irracional.
Ele existe, no entanto, o que o torna real. Por isso, os irracionais – assim como os reais, fazem parte de um conjunto numérico maior que é o conjunto dos números reais.
Curiosidades sobre os números racionais
Há alguns fatos que geralmente confundem as pessoas a respeito dos números racionais que também são parte de outros conjuntos numéricos, e é sempre importante resolver essas dúvidas.
O número 6, por exemplo, é um número natural. É, portanto, inteiro, racional e real. Mas se a definição de número racional é poder ser expresso em uma fração simples não denominada por zero, como isso pode ser verdade? A resposta é simples e óbvia, mas exige algum conforto com conjuntos numéricos: o 6 pode ser expresso como 6/1, certo? Então ele é, por óbvio, racional, e a fração que o expressa está demonstrada – assim como poderia estar em 36/6, ou 72/12.
Seguindo a mesma lógica, números gigantescos expressos em frações – ou que possam ser expressos em frações – são tão racionais quanto os pequenos, e um número que não esteja expresso em frações não é mais ou menos racional que outro. Expressar 3/6 é absolutamente tão racional quanto expressar 0,5.
Um fato curioso sobre o tema é que os números irracionais foram sugeridos na Grécia Antiga por um aluno do famoso Pitágoras. Pitágoras acreditava que todos os números eram racionais, mas um de seus alunos mostrou, através da geometria, que não se poderia expressar a raiz quadrada de 2 em uma fração, o que a tornava irracional. Mesmo com a demonstração, muitos dos seguidores de Pitágoras não aceitaram a explicação, e levou muito tempo para a chegada a um consenso sobre o tema.








Comentar