A teoria dos conjuntos data do século XIX, e foi desenvolvida inicialmente pelo matemático russo Georg Cantor. Sua ideia é possibilitar a associação de certos termos dentro de um conjunto, baseado em características comuns observadas nestes elementos.
No século XX, as teorias originais de Cantor foram complementadas, de modo que a teoria dos conjuntos ganhou bastante robustez, e os paradoxos contidos nela fossem lidados de forma mais simples. A teoria dos conjuntos, por si só, é essencialmente conceitual. Ela permite a definição de certos elementos. Sua grande capacidade prática, no entanto, é servir como base para diversos outros temas mais complexos, como probabilidade e funções.
A teoria dos conjuntos também foi chamada de teoria ingênua ou teoria intuitiva. Isso ocorria porque, como um método de definição de elementos, não era raro que as mais óbvias conclusões fossem obtidas através do seu processo analítico. Dizer, por exemplo, que dois conjuntos são iguais se possuírem os mesmos elementos, é um resultado de análise através da teoria dos conjuntos. Embora pareça bobo, é necessário que exista um conceituação matemática que defina essa premissa, como fez Cantor.
Saiba mais sobre a teoria dos conjuntos, como ela é utilizada e quais são seus elementos mais comuns:
Características dos conjuntos
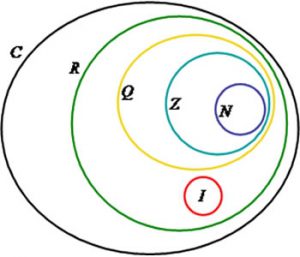
Conjuntos são grupos numéricos que podem ser finitos ou infinitos. Os conjuntos podem ser desde os elementos típicos definidos como Naturais, Inteiros, Racionais, Irracionais e etc., como novos conjuntos, definidos para um propósito.
Um conjunto finito é definido por seus elementos listados separados por vírgulas e encerrados. Os conjuntos infinitos podem ser representados da mesma forma, com a adição de reticências como último elemento, ou através da identificação das propriedades que geram o pertencimento ao conjunto em questão.
O primeiro método é denominado listagem, enquanto o segundo é uma definição de regras. Pode-se elaborar um conjunto P infinito de números pares da seguinte forma:
P = {2, 4, 6, 8, 10, 12…}
Ou pode-se definir sua regra, sem a necessidade de listagem:
P = { x | x é par e positivo}
Lê-se: x, tal que x é par e positivo. Em rigor, as duas representações são exatamente a mesma coisa, pois definem o mesmo conjunto.
Elementos da teoria dos conjuntos
Elementos importantes da teoria dos conjuntos, especialmente no que diz respeito à sua análise, são:
Pertinência
O conceito de pertinência é utilizado como sinônimo de pertencimento, na teoria dos conjuntos. Fala-se que um número x pertence a um certo conjunto. Utilizando nosso exemplo anterior, teríamos que 22 pertence ao conjunto P.
Na notação típica da teoria dos conjuntos, fala-se que 22 ∈ P (Lê-se 22 pertence a P); O contrário também pode ser indicado, de forma que seria anotado que 21∉ P (Lê-se: 21 não pertence a P).
Subconjuntos
Subconjuntos são conjuntos que pertencem integralmente a um outro conjunto mais amplo. Pode-se dizer, por exemplo, que o conjunto dos números Naturais é um subconjunto dos Números Inteiros, pois todos os números Naturais pertencem, também, ao conjunto dos Inteiros.
União
A união é uma espécie de operação dentro da teoria dos conjuntos, embora não se possa considerar como tal. A união ocorre quando um terceiro conjunto reúne todos os elementos presentes em outros dois conjuntos – que, neste caso, seriam ambos subconjuntos deste terceiro conjunto união, mas não possuem – necessariamente uma relação ente si.









Comentar