Mesmo que não lembre, você certamente já ouviu falar em um famoso filósofo grego, chamado Tales de Mileto, criador de um importante método: o Teorema de Tales. O filosofo foi, também, matemático e astrônomo de grande importância, precedendo os nomes mais famosos, entre 624 e 558 antes da Era Comum.
Seu Teorema é amplamente conhecido como uma importante ferramenta de compreensão da geometria, e seu uso ainda é feito nos dias atuais, através de ferramentas mais avançadas.
Entenda o que é o Teorema de Tales, seu conceito e sua forma de aplicação:
O que é o Teorema de Tales?
O Teorema de Tales é uma teoria de geometria aplicada. Ele trata da relação proporcional entre retas paralelas e transversais. Tales de Mileto desenvolveu sua teoria a partir da observação de um pirâmide e sua sombra.
Mais especificamente, observando a pirâmide Quéops, no Egito, o matemático foi capaz de calcular, a partir da sombra que projetava no chão, qual seria a altura reta da pirâmide. Surpreendentemente, a partir deste cálculo, Tales acertou sua altura.
É por isso que é considerado, nos dias atuais, o Pai da Geometria Descritiva. Seu teorema é base para cálculos de distâncias até os dias atuais, sendo um dos princípios fundamentais para questões de razão entre distâncias.
O que diz o Teorema de Tales?
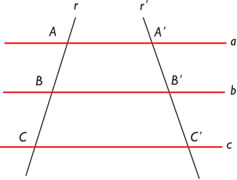
Segundo o Teorema de Tales, entende-se que: “a intersecção entre duas retas paralelas e transversais formam segmentos proporcionais.”. O enunciado pode não parecer exatamente claro, para quem não está acostumado com geometria, mas a compreensão é razoavelmente fácil.
Colocando em outras palavras, isso quer dizer que retas paralelas que cruzem dois pontos transversais irão gerar intersecções, por óbvio. Quando as intersecções da primeira reta são divididas entre si, a razão desta divisão será idêntica à razão das duas intersecções de qualquer outra reta paralela colocada sobre esta mesma forma.
No caso de Tales, imagine a pirâmide Quéops, no Egito. Sua sombra projetava um triângulo no chão. A percepção do filósofo foi de que se ele traçasse uma reta segmentando uma parte próxima ao topo da projeção e dividisse o valor dos dois pontos de intersecção, a razão encontrada seria idêntica à razão dos dois pontos de intersecção de uma reta traçada próxima à base da sombra. Isso permitiu que ele identificasse uma proporcionalidade na forma, tornando-a mais fácil de ser mensurada.
O mesmo pensamento seria válido, portanto, pensando na projeção de um triângulo com vértices na ponta da pirâmide, na ponta da projeção e no ponto da base sob seu topo.








Comentar