Binômio de Newton é o nome dado à complementação que Isaac Newton deu ao campo dos produtos notáveis. Na prática, o tão famoso binômio de Newton nada mais é do que a percepção do que hoje é chamado de “primeiro caso de produto notável”, em várias fontes.
Em geral, é o primeiro tipo de produto notável aprendido durante o estudo do conteúdo. A boa notícia é que se o nome binômio de Newton assusta você, não há motivos para isso. A existência de um produto notável possui exatamente a finalidade de facilitar a realização de um cálculo complexo através da identificação de expressões comuns na matemática.
O binômio de Newton dedica-se ao que chamamos de o quadrado da soma de dois termos, em um conteúdo de produtos notáveis, mas pode elevar-se a diversas outras potências, para além do quadrado, aumentado sua complexidade.
Entenda o que é este produto notável, qual é sua utilidade, e como chegar aos resultados de cálculos de forma mais rápida através dele:
O que são os produtos notáveis?
Produtos notáveis nada mais são do que polinômios comumente encontrados em expressões algébricas diversas. O nome “produto notável” refere-se justamente ao fato de que estes polinômios são notados com frequência na matemática.
A percepção da comunidade é que um polinômio sempre resulta em um produto final igual, de acordo com seus termos. Assim, saber a forma de seu resultado evitaria que o matemático precisasse calcular – toda vez – o produto de um polinômio, chegando imediatamente ao seu resultado assim que o identificasse.
O Binômio de Newton é um polinômio identificado como o quadrado da soma de dois termos, em suas versões mais simples, mas aplicando-se – também – a binômios semelhantes com outras potências, como aqueles elevados ao cubo.
Binômio de Newton elevado ao quadrado
O exemplo mais clássico do binômio de Newton é a sua elevação ao quadrado. Como já definido em nosso artigo sobre produtos notáveis, trata-se de uma típica situação de quadrado da soma de dois termos. Essa situação pode ser matematicamente expressa por:
(a + b)2
Toda vez que este caso aparece em uma expressão algébrica, é inevitável que seu resultado seja:
a2 + 2 . a . b + b2
Saber, portanto, que (a + b)2 = a2 + 2 . a . b + b2 é o primeiro tipo de produto notável. O exemplo auxilia na exemplificação, ainda, da utilidade destes produtos notáveis: saber disso poupa o estudante a fazer todo o processo de cálculo, sempre que encontrar este produto.
Em uma situação em que este produto notável é encontrado e em que a = 2, pode-se racionar o seguinte:
(2 + b)2 =
Sabe-se que o resultado deste produto notável é o quadrado de cada um dos termos mais 2 vezes o produto dos dois termos (neste caso 2.2b), como demonstrado acima. Portanto, o resultado é
4 + 4b + b2, sem a necessidade de realizar todo o processo de multiplicação. Este é o processo de substituição que você deverá fazer toda vez em que encontrar tal produto notável.
Elevação por potências mais altas
O binômio de Newton, no entanto, não resume-se apenas a expressões elevadas ao quadrado. Ele possui validade para qualquer potência. Neste caso, há uma relação de escalonamento. A resolução de uma potência sempre corresponde ao resultado do binômio de Newton na potência anterior multiplicado por mais uma soma dos termos.
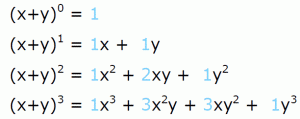
No caso do cubo da soma de dois terços, o cálculo a ser feito é o resultado do binômio quadrado do trecho anterior multiplicado por (a + b). Significa dizer, portanto, que:
(a + b)3 = (a2 + 2ab + b2) . (a + b)
Seu resultado, portanto, seria:
a3 + 3a2b + 3ab2 + b3
Significa dizer, também, que elevar este binômio à quarta potência equivale a multiplicar o membro (a3 + 3a2b + 3ab2 + b3) por (a + b), e elevar o binômio à quinta potência significa multiplicar a relação deste produto da quarta potência por (a + b) novamente, e assim por diante.








Comentar