Uma progressão geométrica pode ser utilizada em diversas situações, incluindo em nosso dia a dia, quando raramos pensamos estar fazendo matemática propriamente dita. É comum imaginarmos quando custaria ou quanto lucro teríamos se um produto ou serviço custasse outro valor, e fazer um exercício de escalonamento de forma simples.
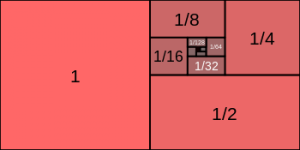
Isso porque uma progressão geométrica nada mais é do que uma sequência numérica baseada em uma certa razão constante. Significa que se você começa a calcular quanto lucro teria vendendo x produtos, depois o dobro de x e depois o dobro deste novo valor, por uma questão de curiosidade, estabeleceu uma progressão geométrica sem nem mesmo perceber.
Entenda o que é essa área da matemática, suas definições e usos:
Conceito de progressão geométrica
Uma progressão geométrica é uma sequência formada por números que, salvo o primeiro termo, é definido a partir da utilização de uma razão constante. Essa razão é a responsável por definir todos os termos seguintes após o primeiro. De forma geral, progressões aritméticas são formadas pela multiplicação entre o termo atual e a razão.
A razão das progressões geométricas podem ser definidas por qualquer número, desde que dentro do conjunto dos racionais e desde que não seja o zero. Para exemplificar uma sequência geométrica, pode-se pensar em uma sequência iniciada pelo termo 1, infinita, com razão 2. Essa sequência seria:
(1, 2, 4, 8, 16, 32, 64, 128, 256, 512, …)
Cálculos sobre progressões geométricas
Existem vários cálculos que podem ser utilizados para a compreensão de progressões geométricas. O mais simples dele, sem dúvidas, é o cálculo de definição de termos seguintes. Trata-se da multiplicação do termo atual pela razão da progressão.
Em outras palavras, sendo a o termo atual e r a razão, pode-se definir que
a2 = a1 * r
Além disso, outro cálculo importante neste conteúdo é a fórmula de definição do termo geral, que permite descobrir o valor de qualquer termo, sendo n a posição do termo dentro daquela sequência:
an = a1 * r(n – 1)
Tipos de progressão geométrica
Há basicamente quatro categorias entre as quais as PGs podem ser divididas, de acordo com o tipo de razão definida para ela. A razão sempre é o elemento definidor da natureza das progressões geométricas.
Os tipos de progressão geométrica são:
Progressões geométricas oscilantes
Uma PG oscilante é aquela em que a sequência numérica por ela definida é composta por números que intercalam sinais positivos e negativos a cada novo termo. Isso ocorre em função de a razão desta progressão ser negativa.
Progressões geométricas crescentes
Uma PG crescente é aquela em que a sequência numérica, por óbvio, é crescente. Nestes casos, a razão é sempre positiva. Em caso de sequências positivas, é necessário que a razão seja maior do que 1, enquanto em sequências negativas, é necessário que 0 < r < 1.
Progressões geométricas constantes
São aquelas em que a sequência numérica é composta por termos idênticos. Este tipo de progressão geométrica só ocorre quando a razão é igual a 1.
Progressões geométricas decrescentes
São aquelas nas quais cada termo é menor que seu termo anterior. Nos casos de sequências positivas, isso ocorre quando a razão é um número positivo inferior a 1. Nas sequências negativas, a condição estabelecida é que a razão seja superior a um.
Propriedades de uma progressão geométrica
Existem diversas propriedades importantes para a definição de uma progressão geométrica. Essas propriedades facilitam na compreensão destas sequências e na familiaridade com seus atributos.
Entre essas propriedades, há o fato de que a divisão de um termo da sequência por seu termo anterior resulta, sempre, na razão definidora daquela PG. Trata-se de uma das propriedades mais importantes com utilidade prática no cálculo de uma progressão deste tipo.







Comentar